The history of tuning and temperament in the western music culture.

Our occidental or western music has a particular feature, distinguishing it from most of the other music cultures:

The polyphony!




This traditional polyphony is based on layers of third and fifth intervals. Typical examples are major and minor triads. These chords will only sound convincing, when their specific tones are tuned to ideal frequency relations.

The fifth, the primal interval.


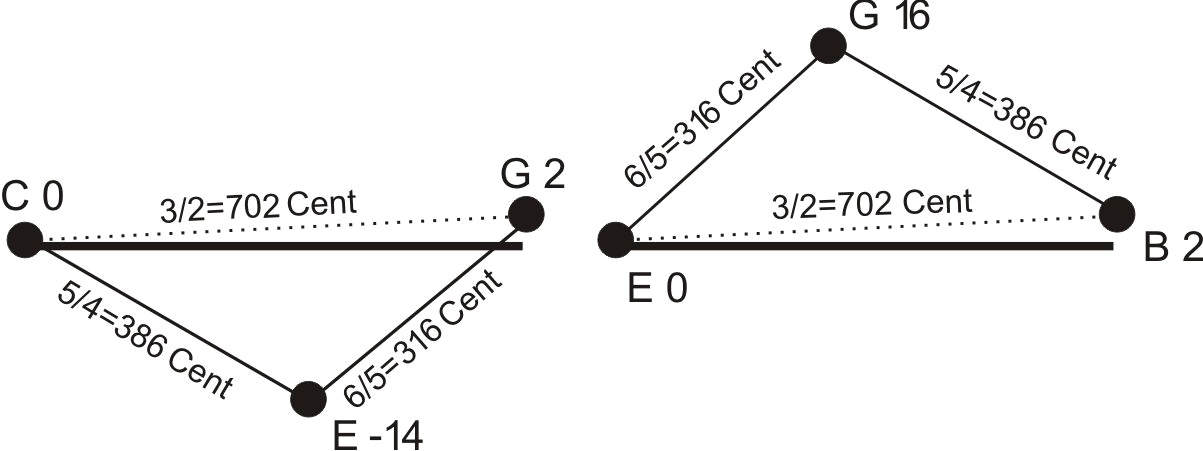
The two mentioned and most important chords of the western music culture consist of a fifth interval, divided into a major and a minor third. In the basic position, the major chord has the major third in the lower and the minor third in the upper position. For the minor chord it is reversed. By the way: The thirds have only been considered as independent intervals for about 800 years. This was connected with the emergence of the major and minor chords. Before that, only fifths have been used as musical components. Therefore, we will start with the fifths.

The two specific tones of a fifth interval should ideally be tuned to a frequency ratio of 3 : 2. For example E = 660 Hz, A = 440 Hz.

Listen here to a fifth interval. It begins in just intonation, drifts to detuning and then back to just intonation.

A fifth with the ideal frequency ratio of 3 : 2 however is a bit wider than a usual tempered fifth: 702 instead of 700 Cent. Since we use the calculation unit Cent more often, we will explain this arithmetic unit in the following.

Insertion: The Cent Calculation


Calculating and depicting different tuning models on the basis of frequency ratios is a tedious work. One has to multiply and to divide, and one cannot distinguish different outcomes at a glance. It is for this reason that the Cent calculation was invented. It is easy to understand.

Looking at a piano keyboard, you recognize that each octave consists of 12 steps. If (as usual) the instrument is tuned to equal temperament by an equal frequency ratio from each key to the next, you could term the frequency distance between adjacent tones as “One Halftone” or “1 HT”. A fifth interval hence could be called 7 HT, a major third interval 4 HT.

Since non-equal-tempered tuning models require a more detailed calculation basis, one has divided the value “1 HT” into 100 equal tempered frequency distances. This new calculation unit is called “Cent”. 1 HT has 100 Cent, the Octave 1200 Cent, the equal tempered fifth 700 Cent. But a fifth in just intonation has a value of 702 Cent.

Note: Cent never designate absolute frequencies, they designate frequency distances.

If you want to calculate the corresponding Cent value from a frequency ratio yourself, create an Excel table as follows:
Frequency 1 in Hz
Frequency 2 in Hz
(Result) =(LOG(Frequency 1)-LOG(Frequency 2))/LOG(2)*1200
Here is an example for the fifth in just intonation:
Frequency 1 = 3
Frequency 2 = 2
=(LOG(3)-LOG(2))/LOG(2)*1200
Result: 701,955… rounded to 702 Cent

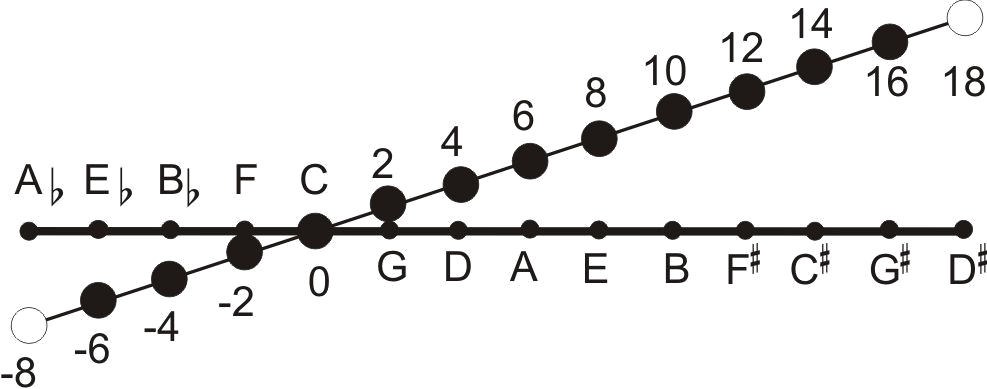
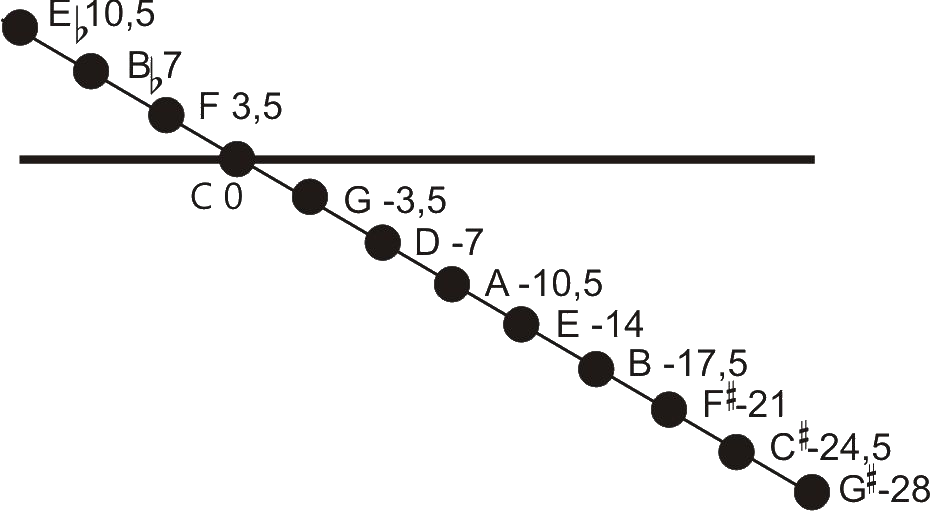
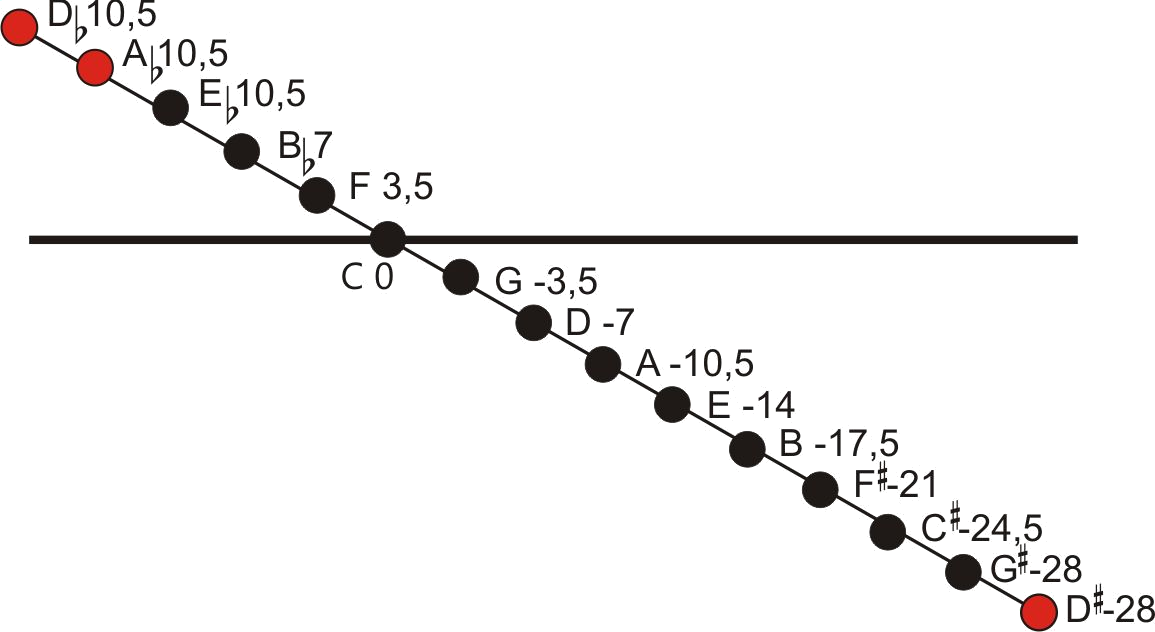
Continuation: The fifth, the primal interval. In the following diagram the tuning values of equal temperament are shown as a horizontal line. The sequence of fifths in just intonation with their tuning values of 702 Cent differ from this line. This fifths sequence does not give a closed system, A-flat, for example, differs from G-sharp by 24 Cent. This difference is called the "Pythagorean comma". Why?

The term "Pythagorean comma" is based on the fact that we trace back this musical system to the Greek philosopher Pythagoras and his followers, the Pythagoreans. In the 6th century BC, they developed a musical system based on pure fifths. It is said they measured pitches with the help of a monochord. By dividing its string to a length ratio of 2 : 3, they detected a very pure sounding interval, the fifth.

The Pythagoreans, however, were not the first ones whose music system was based on pure fifths. More than 2,000 years earlier, the Chinese had a music system basing on pure fifths. It is said that it was developed by Confucius, by using flutes made of bamboo tubes. This system included 5 tones per octave. Such a music system is called "pentatonic".

Starting on the left, each flute is duplicated. The duplicate flute is shortened by 1/3 of its length, thus creating an upper fifth. As soon as a newly created fifth jumps to the next higher octave, the flute length will be doubled so that this new fifth will be positioned in the starting octave. (See the examples d-D and e-E).

However, such music systems based on fifths were developed still much earlier. Here you can see the picture of a prehistoric flute, found in a cave in southern Germany. It is about 30,000 years old. This sheds a whole new light on the cultural height of our ancestors.

The pitches of the different tones of this flute can be derived from the fifth sequence D-A-E-B. If the pitch of the broken end was tuned to G, which is very probable, it would be the five notes G-B-D-A-E, according to the pentatonic scale G-A-B-D-E.

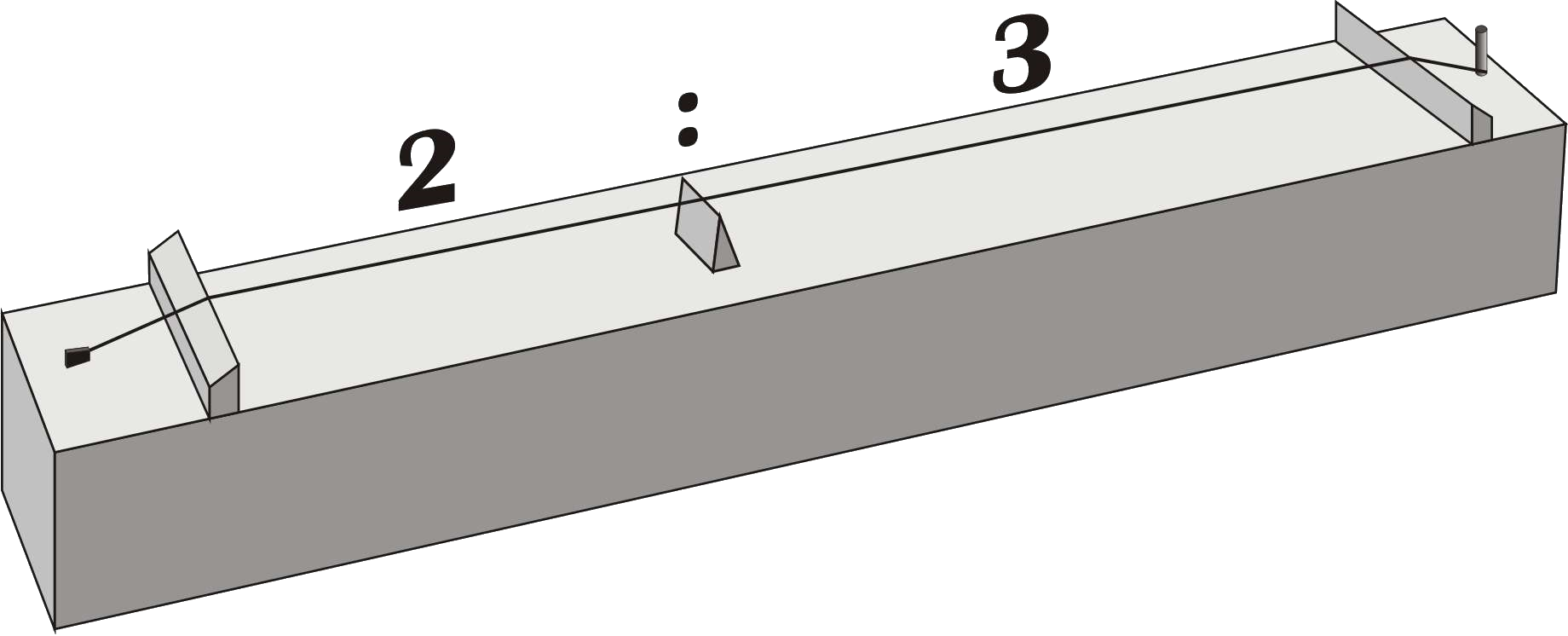
Incidentally, the tone holes of this flute are not drilled, but scraped, so that the pitches could be tuned higher or lower as they were created. This suggests that there was a reference instrument to which this flute were adapted.

This is how a melody played on this flute could have sounded. To this day, the melodies of many of our children's songs are pentatonic and probably come from prehistoric times.

Let us go back, or rather go forward again to the Pythagoreans: Their tuning system, based on purely tuned fifths, formed the relevant theoretical and practical musical system in Europe until the end of the twelfth century. The thirds were of no interest to the Pythagoreans. Indeed, there existed also ideas for purely tuned thirds, but because of their different pitch, they would have disrupted the Pythagorean tuning model. The ideal of the Pythagoreans was an unambiguous system, which should also support their community.

Listen here to a musical example from the time around 1200, presented with Pythagorean tuning.

Still fully adherent to the Pythagorean ideal, only the empty fifth is regarded as a complete consonance.
At the beginning of the penultimate measure, surprisingly there is a B-flat major chord, which, contrary to our current musical conception, is supposed to build up a tension, leading to the dissolution by the final fifth interval.

In the thirteenth century English singers experimented with pure tuned thirds and inserted them into the musical texture. Listen here to a canon from that time: „Sumer is comen“, with fifths and - as a novelty - thirds in just intonation.
For our ears this sounds quite normal, but for the musicologists and key instrument makers of that time, it was an unpleasant surprise, almost a catastrophe.
Why?

Thus the disorder, feared by the Pythagoreans, had arrived.

Tones with the same name had to be tuned to different pitches, depending on their harmonic function, depicted here by the example of an "E". Its higher position originates from the continuous fifth sequence C-G-D-A- E. The deeper position shows its pitch when tuned directly to the C as a pure tuned major third. This deeper pitch is calculated from the frequency ratio E : C = 5 : 4 with the result of 386 Cent. The pitch difference between both positions is 22 Cent, the so-called "Syntonic Comma”.

Major and minor chords, with fifths and thirds both tuned to its specific just intonation, are pictured in the adjacent figure.

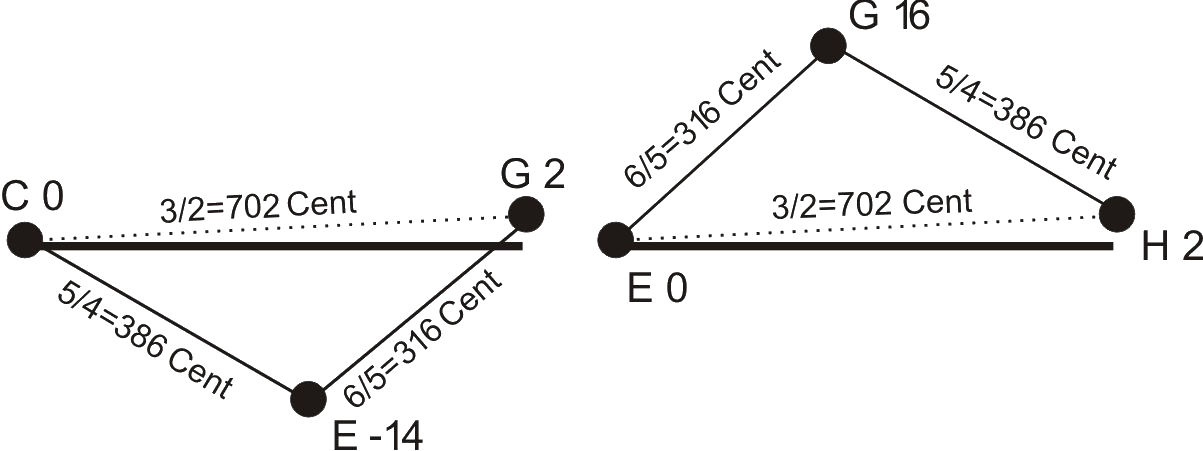
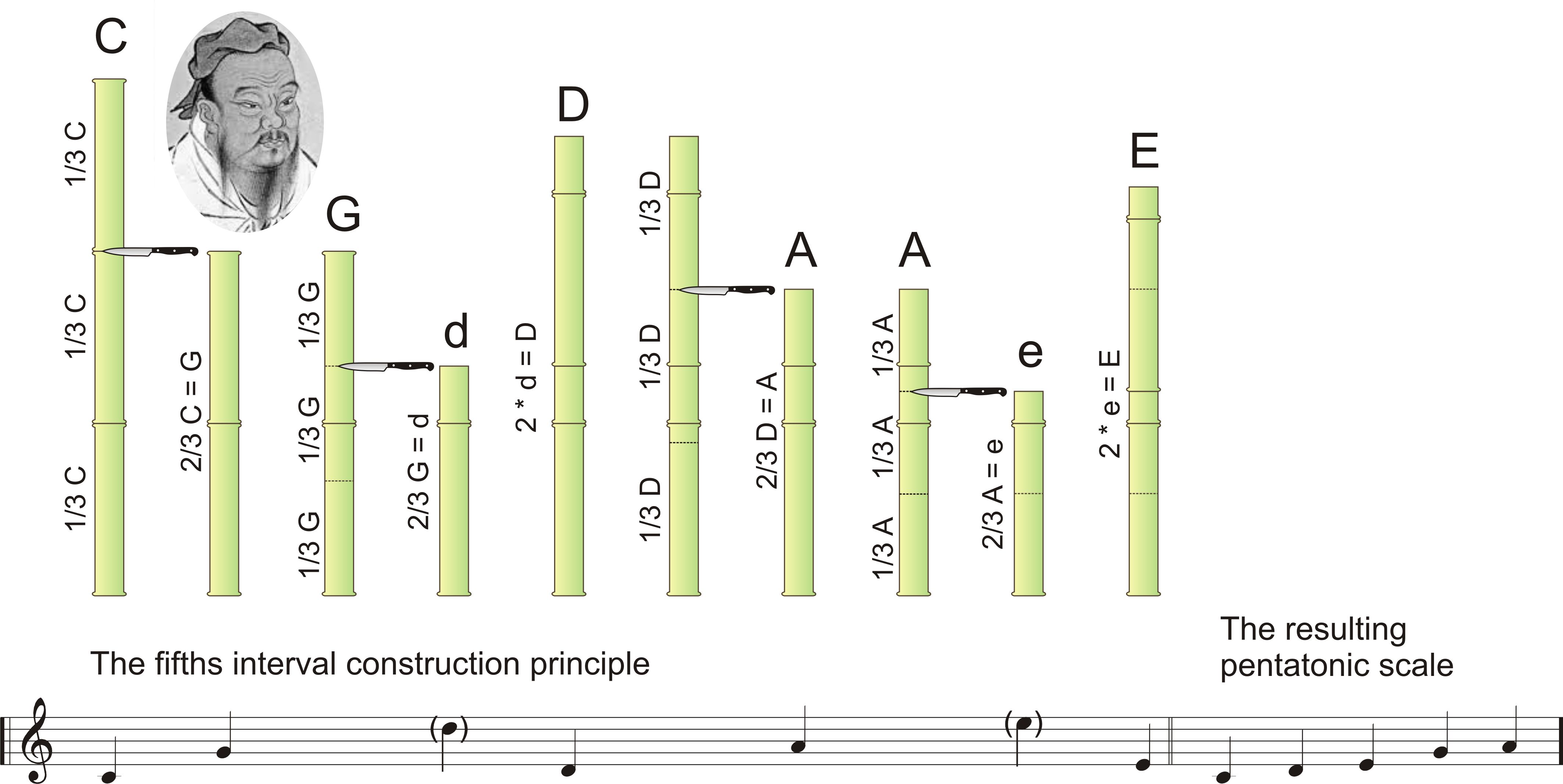
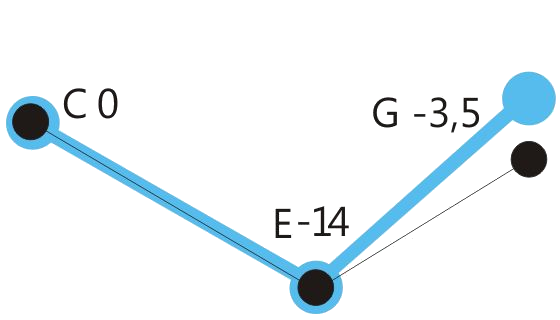
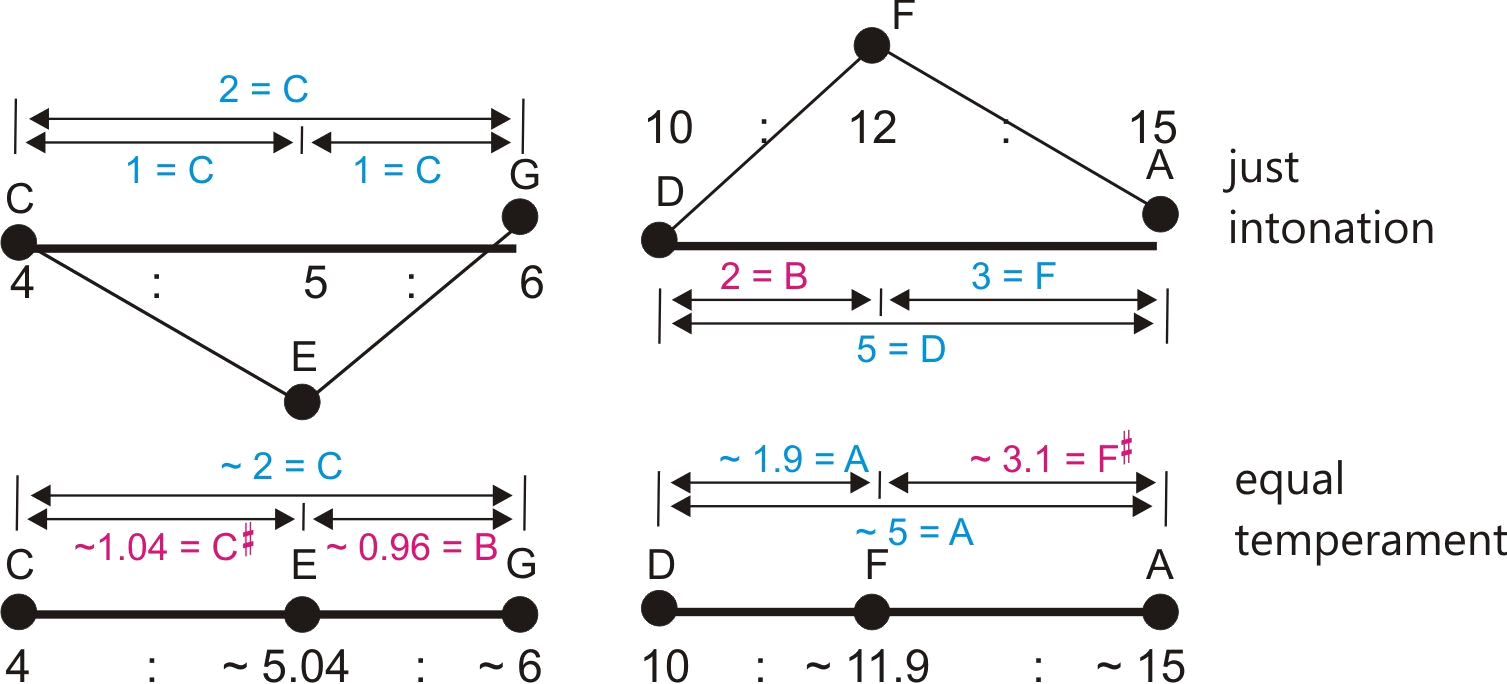
Building a tuning model with continuous fifths and thirds in just intonation already fails at the attempt to create a simple diatonic scale with its seven different tones. Here, it is illustrated by the example of C major:

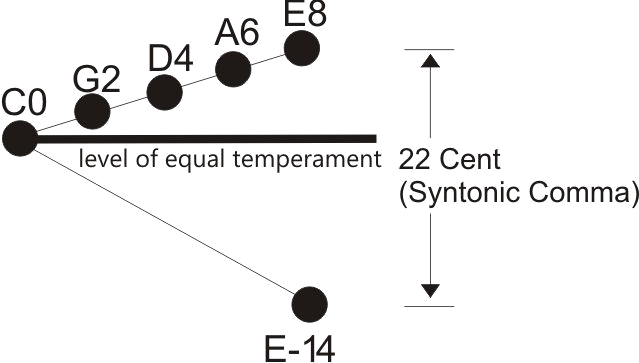
For the second tone of this scale, the D, one needs two different positions: A higher one for the chord G_B_D and a deeper one for the chord D_F_A. The pitch difference is 22 cents, the already mentioned "Syntonic Comma”.

In order to deal with the problem, musical theorists and key instrument builders developed a new tuning system in which the fifths were narrowed in a way that a sequence of thirds in just intonation resulted.

The fifths were tuned tighter by a quarter of the Syntonic Comma (i.e. 5.5 Cent), so that after four fifths steps a major third in just intonation was created. Therefore, this tuning method is called 1/4 Comma Meantone. Meantone - because within a major third in just intonation, for example C_E, the whole-steps, here C_D and D_E, are equally tuned.

Der erste Nachteil des mitteltönigen Stimmungsmodells besteht darin, dass es ebenso wie das pythagoreische kein geschlossenes System bildet. Im oben dargestellten Modell für die üblichen 12 Töne je Oktave sind nur die Dur-Dreiklänge von Eb-Dur bis E-Dur terzenrein gestimmt. Man kann damit also nur in den Tonarten B–Dur bis A-Dur und den entsprechenden Mollparallelen musizieren. Erfahrene Cembalospieler stimmen jedoch je nach Bedarf das G# zum Ab hoch oder das Eb zum D# hinunter . Bei manchen Instrumenten hat man auch ergänzende Halbtöne wie Db, Ab oder D# (sogenannte Subsemitonien) in die Tastatur eingefügt. Siehe die rot gezeichneten Töne im Diagramm unten. Dafür wäre eine Tastatur mit 15 Tönen je Oktave notwendig.
Der zweite Nachteil ist, dass die Quinten der terzenrein gestimmten Akkorde notgedrungen zu eng gestimmt sind und dadurch, je nach effektiver Tonhöhe, mehr oder weniger schnell schweben.
Der dritte Nachteil ist, dass viele Blasinstrumente, besonders in tiefen Lagen, Schwierigkeiten haben, den teilweise sehr hoch, teilweise sehr tief gestimmten Töne mitteltönig gestimmter Tasteninstrumente zu folgen.

Ein wesentlicher Grund für den Reinheitseindruck unterschiedlich gestimmter Akkorde beruht auf den Differenztönen, welche durch die akustische Überlagerung gleichzeitig erklingender Töne entstehen. Deren Frequenz lässt sich ganz einfach errechnen aus
"Tonhöhe des höheren Originaltones minus Tonhöhe des niedrigeren Originaltones".
Hier am Beispiel eines A-Dur Akkordes veranschaulicht. Die Originaltöne sind in Schwarz dargestellt, die Diffenztöne dagegen in Grau.

Bei reiner Stimmung (Just intonation) stimmen alle Differenztöne oktavenrein zu den Originaltönnen, bei pythagoreischer Stimmung stimmt zwar der Differenzton des Quintintervall oktavenrein, die Differenztöne der großen und der kleinen Terz sind dagegen um insgesamt 10 Cent verstimmt. Bei der mitteltönigen Stimmung stimmt der Differenzton der großen Terz oktavenrein, die der Quinte und der kleinen Terz sind insgesamt um 4,2 Cent verstimmt, also insgesamt deutlich weniger als bei pythagoreischer Stimmung.

Hören Sie hier ein kurzes Musikbeispiel in pythagoreischer, mitteltöniger und umfassend terzen-und quintenreiner Stimmung an. Umfassend terzen- und quintenrein ist allerdings bei Tasteninstrumentenn nur möglich, wenn sich deren Stimmung programmgesteuert an die jeweilige harmonische Situation der dargebotene Musik anpasst. Eine erste Orgel mit einer solchen Technologie ist mittlerweile erbaut, wir kommen im Folgenden noch darauf zu sprechen.

Der herkömmlichen Tasteninstrumenten eigene Konflikt zwischen Quinten- und Terzenreinheit betrifft nicht Streicher, Bläser und Sänger, weil diese, wenn gut geschult, gleichzeitig mit reinen Quinten und reinen Terzen intonieren können. Trotzdem bezeichnen manche Musikwissenschaftler eine von Streichern, Bläsern und Sängern quinten- und terzenrein dargebotene Musik als "mitteltönig intoniert". Schuld an dieser unsinnigen Bezeichnung ist, dass die Musikwissenschaft traditionell sich mit festen Stimmungsmodellen beschäftigt. Eine variable Stimmung passt nicht zu dieser Denkweise.

Da wir schon dabei sind, fragwürdige Aussagen zu erwähnen: Es gibt Musikwissenschaftler und Organisten, welche die Meinung vertreten, dass das, was aus der Renaissance-Zeit als a-Capella-Gesang überliefert ist, immer nur mit Begleitung eines mitteltönig gestimmten Tasteninstrumentes aufgeführt worden sei. Wenn man jedoch die Madrigale eines Gesualdo mit ihrer schweifenden Harmonik betrachtet, so erkennt man, dass man diese weder mit einer mitteltönigen Stimmung noch mit irgend einem anderen festen Stimmungsmodell kompetent begleiten kann.

Weil das mitteltönige Stimmungsmodell Probleme macht, sobald man in entferntere Tonarten modulieren oder springen will, forderten vom 17. Jahrhundert an immer mehr Komponisten dass es möglich sein sollte, auf Tasteninstrumenten auch in entferntere Tonarten zu modulieren. So wurden neue, geschlossene Stimmungsmodelle entwickelt. Allerdings wurde nicht gleich zur gleichstufigen Stimmung übergegangen, sondern sogenannte „Temperaturen“ entwickelt, welche wenigstens in der Mitte des Quintenzirkels reinere Terzen bereithielten. Ein typisches Beispiel zeigt „Kirnberger III“, wie nachstehend dargestellt.

Von C bis E läuft eine mitteltönig gestimmte Quintenreihe abwärts, ab da geht es ungefähr pythagoreisch gestimmt wieder aufwärts.

Andreas Werckmeister schlug als einer der ersten am Ende des 17. Jahrhunderts solche Stimmungsmodelle vor. Er nannte sie „wohltemperiert“. Damit nahm er eine heute noch gern verwendete Marketingmaßnahme vorweg: Eine problematische Angelegenheit mit einem wohlklingenden Namen zu belegen. Man nennt so etwas einen Euphemismus.

Major and minor chords, with fifths and thirds both tuned to its specific just intonation, are pictured in the adjacent figure.

Building a tuning model with continuous fifths and thirds in just intonation already fails at the attempt to create a simple diatonic scale with its seven different tones. Here, it is illustrated by the example of C major:

For the second tone of this scale, the D, one needs two different positions: A higher one for the chord G_B_D and a deeper one for the chord D_F_A. The pitch difference is 22 cents, the already mentioned "Syntonic Comma”.

In order to deal with the problem, musical theorists and key instrument builders developed a new tuning system in which the fifths were narrowed in a way that a sequence of thirds in just intonation resulted.

The fifths were tuned tighter by a quarter of the Syntonic Comma (i.e. 5.5 Cent), so that after four fifths steps a major third in just intonation was created. Therefore, this tuning method is called 1/4 Comma Meantone.

Meantone - because within a major third in just intonation, for example C_E, the whole-steps, here C_D and D_E, are equally tuned.

Listen to a major chord in three different tunings: Pythagorean, just intonation and meantone.

Heinrich Isaac’s „Innsbruck ich muss Dich lassen“ presented by a meantone tuned organ.

This sounds indeed convincing.

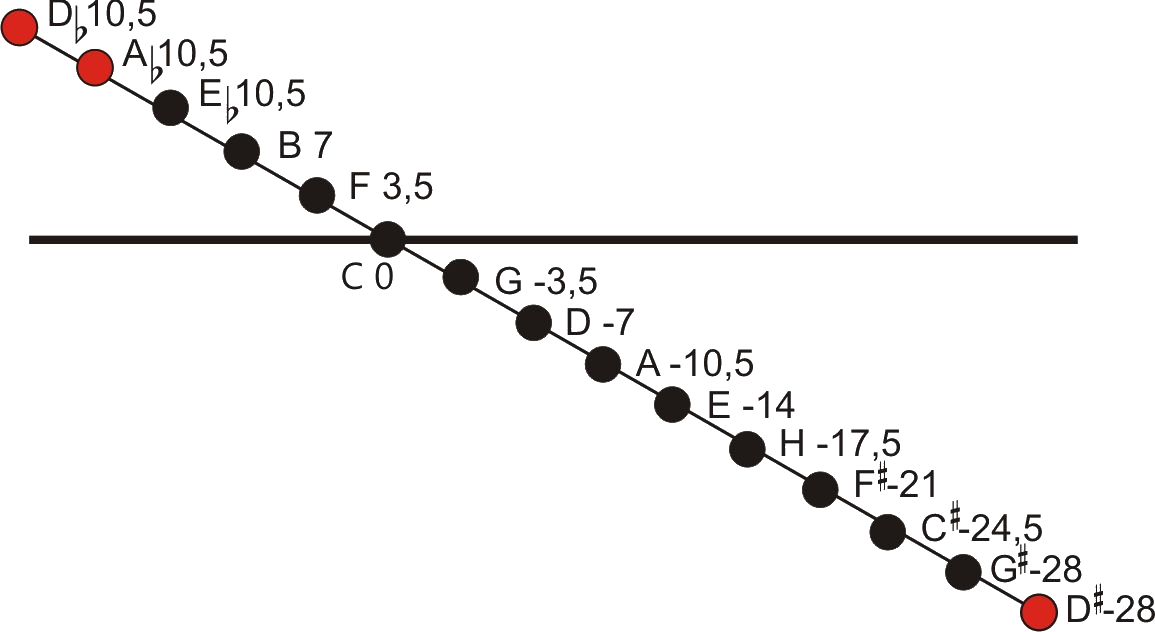
The disadvantage of this tuning model is that, like the Pythagorean, it does not form a closed system. Only the chords from E flat major to E major possess thirds in just intonation. Therefore, only the keys between B flat major and A major and their corresponding minor keys can be used. Sometimes there were attempts to insert additional halftones like A flat or D sharp (so-called subsemitones) into the keyboard’s octave. See the tones drawn in red in the diagram below. Well-trained harpsichord players tune their instruments even today to Meantone. They tune, if necessary, the G sharp upwards to an A flat or the E flat downwards to a D sharp.

From the 17th century onwards, however, more and more composers demanded that it should be possible to modulate within a musical piece to all keys. Therefore, new tuning models have been developed. However, this did not lead immediately to equal temperament. Instead, so-called “temperaments” were developed, giving better tuned thirds in the middle of the circle of fifths. A typical example is "Kirnberger III", as shown below.

From C to E a meantone-tuned fifth sequence moves downwards, from there on the fifths move upwards quasi like Pythagorean tuning.

At the end of the 17th century Andreas Werckmeister was one of the first to propose such tuning models. He called them "well-tempered". Thus, he anticipated an actual marketing strategy: Providing a problematic affair with a well-sounding name. This is called an “Euphemism”.

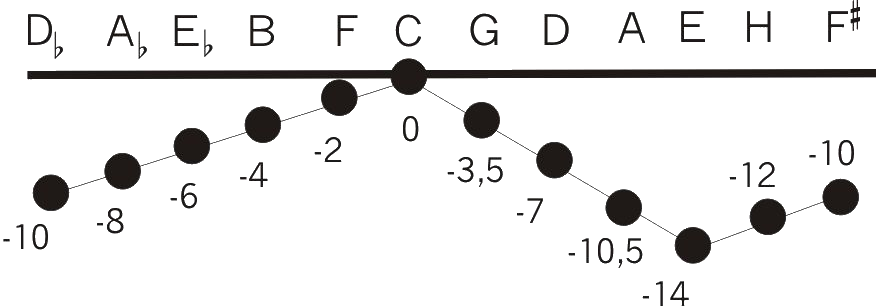
The problem of the “well-tempered“ tuning systems are the partly poor tuned thirds. Especially the major chords of the keys with many accidentals sound sharp and rough. By contrast, all minor chords sound acceptable. Why?
The reason for this is: For minor chords two different ideal tuning methods exist.



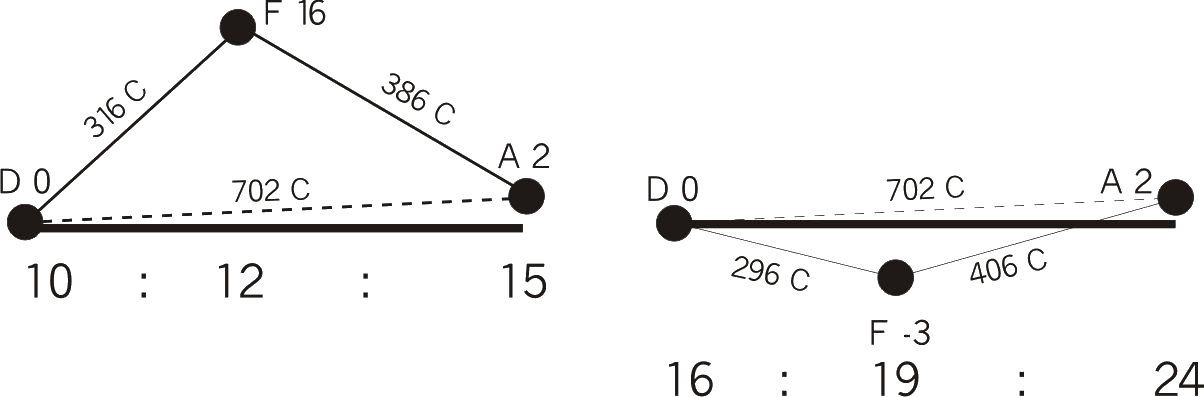
The chord on the left it is built with the same thirds like the pure tuned major chord, the one on the right it is constructed with alternate thirds. For this alternate version, all frequencies are positioned close to equal temperament (the horizontal line). With well-tempered tuning systems all minor chords are tuned near either to the first or to the second ideal. Unfortunately it is not possible to use the alternate minor thirds for major chords, they would still sound strange.

Listen to a minor chord in three different tunings: Traditional just intonation (10 : 12 : 15), equal tempered and the alternative purity (16 : 19 : 24).All three sound useful, including the temperd one due to their proximity to thr alternate version.

Coming back to an unequal tuned temperament with the example of Kirnberger III. See the list of its major chords. The black elements show their effective tuning, the ideal is drawn in blue. The closer the two colors are, the more pleasant the sound. The more distant, the sharper and rougher the sound.

As mentioned above, minor triads can be tuned to two different ideals. Using the thirds of the pure tuned major chord leads to the frequency ratio of 10:12:25, drawn here in blue, the alternate tuning ratio of 16:19:24 is drawn in green. The different minor chords of Kirnberger III, shown in black, come close to one or to the other ideal. A-minor is near to the first alternative, c-minor is near to the second one. You can listen here to both. They present a different chord characteristic.

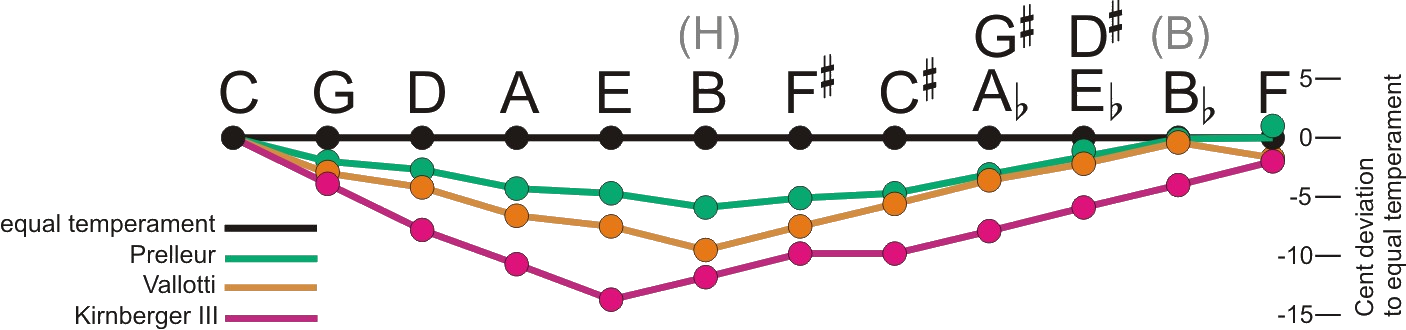
To meet the requirements of an extended tonality, the „well-tempered“ tuning models during the 18th century became more and more similar to equal temperament. Here you can see four of such temperaments, beginning with Kirnberger III and ending with equal temperament. The last one is the actual most common tuning method, all minor chords sound suitable, all major chords sound rough and poor. From a musical point of view this is a topsy-turvy world.

If one complains about the partly poor tuned chords of unequal well-tempered tuning models, some organists reply that the composers of the Baroque period used them for underlining musical messages. Therefore, let us look at J. S. Bach to see whether this can be confirmed.
The last verse of the chorale „Oh Haupt voll Blut und Wunden“ of the St. Matthew Passion begins with the words “Wenn ich einmal soll scheiden” (If I someday shall leave this world) and ends with the words “So reiss mich aus den Ängsten” (So take the fear of me). With other words, the message starts on the earth, underlined by A minor and ends in the paradise by modulating to E major. A-minor sounds quite good in all well-tempered systems, E major, however, sounds rough. It is inconceivable that Bach wanted to depict the paradise by means of poor sounding chords.

Listen to this example firstly with Kirnberger III. Note the rough sound at the end.





Then with Hermode Tuning, controlling also E major with a clear sound.





The second version underlines the sense of the chorale’s words better, the first one works against it.

Differential- or combination-tones

We have already mentioned the differential tones. Most music listeners do not recognize them, although they resonate distinctly at multi-voice music. Differential-tones or combination-tones with less than 18 Hz are not perceived as tones but as beats. (For elephants or whales it may be different).
Tones and beats are in physical terms the same, they are periodical acoustic events. Non-periodical acoustic events are perceived as noise.

Listen here to a gliding differential tone. It begins with the interval A flat-C in just intonation. Then the A flat glides upwards to the C, the differential tone therefore glides downwards. At its deepest position the differential tone changes to beats, caused by the imperfect accordance of the upwards tuned A flat with the C. Then the A flat and the differential tone glide back to their initial positions.

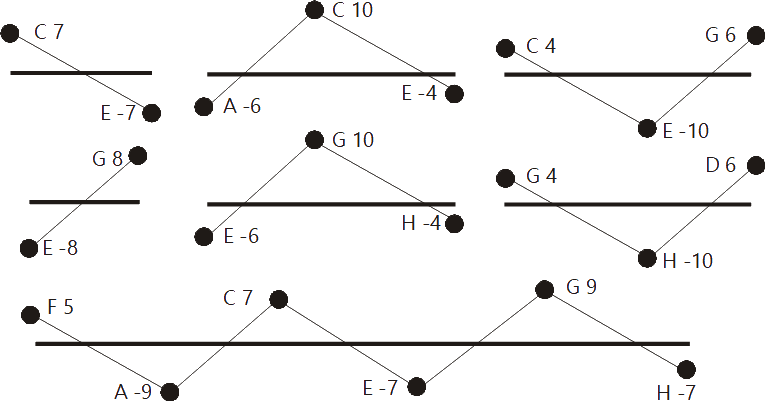
Here a major triad and a minor triad is shown, alternately in just intonation and in equal temperament. The original tones and their frequency ratios are drawn in black, the differential tones and their frequency ratios are drawn in color. Blue means identic to the original tones, red means different from them. The equal tempered examples show a minor triad with only one disturbing differential tone, the major triad, however, shows two of them. In just intonation the major triad shows a perfect situation, the minor triad against this keeps one disturbing differential tone.

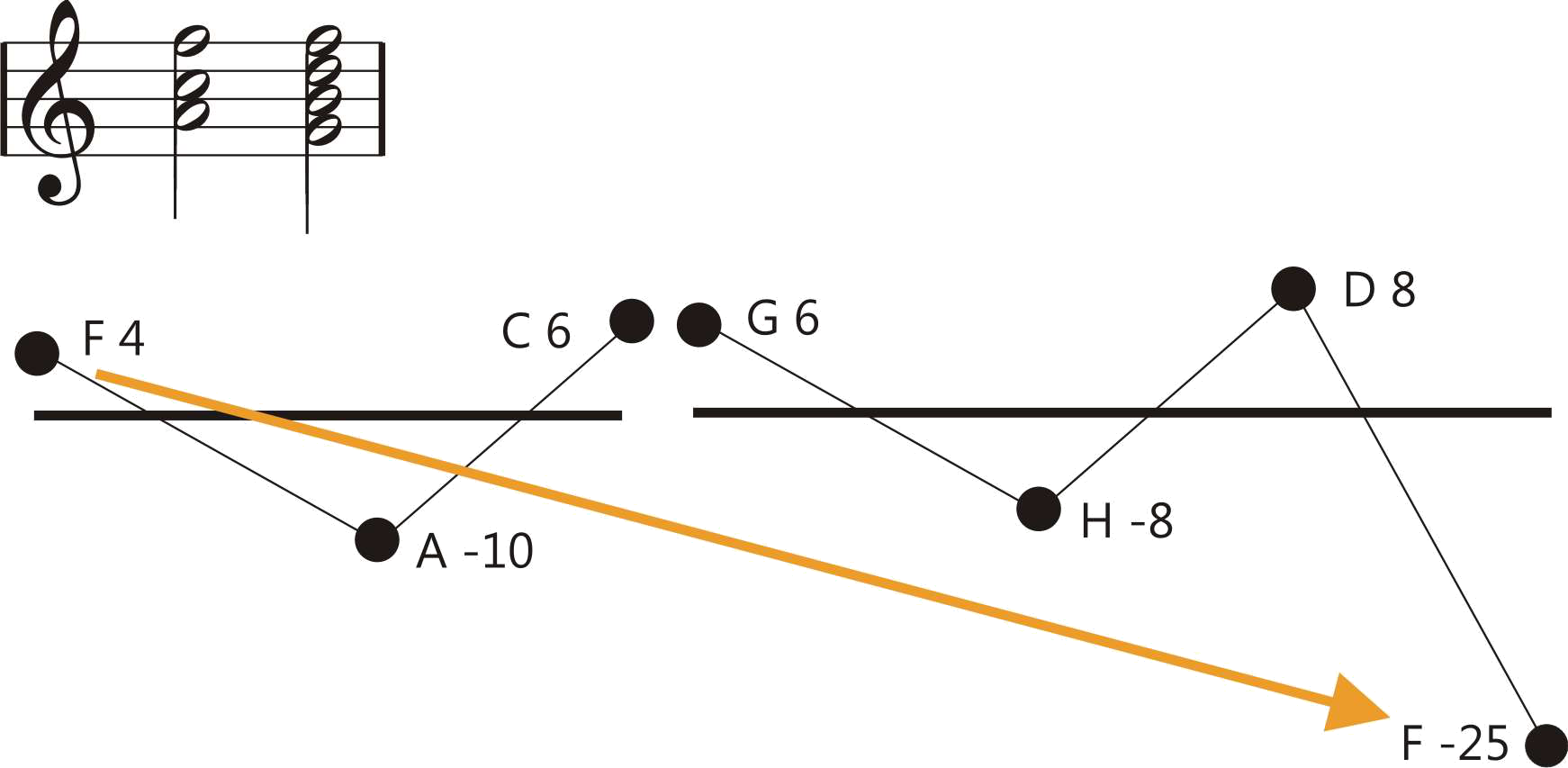
Therefore, when performing a concert for piano and orchestra, it is common practice that the piano plays the equal tempered D minor chord D-F-A for intonating the reference A for the orchestra.


Listen here to an orchestral intonation with the help of the equal tempered d-minor triad D-F-A.

The Natural Seventh

Chords that are made up of perfectly tuned fifths and thirds are usually referred to as "purely tuned".Some musicians also want another interval in pure tuning, namely the seventh in dominant seventh chords. This should be tuned in a ratio of 7: 6 to the root note and thus sounds very strong. The music examples on our "Examples" page, which are marked 3/5/7 at the end of the text, have such tuned dominant seventh chords. Because this seventh is tuned much lower than in equal temperament, however, it can cause problems in the melodic sequence. More on this in the next section. Below you find a sound comparison of differently tuned dominant seventh chords.

The example opposite presents a dominant seventh chord with the following tonic in 3 variations
- pure tuned fifths and thirds, the seventh in a tempered position.
- both chords in equal temperament
- pure tuned fifths and thirds including a natural seventh at the first chord. <

Hermode Tuning as tuning control system

Several attempts have been made for a program-controlled tuning of digital key instruments and of digital music applications. But only Hermode Tuning has become accepted.
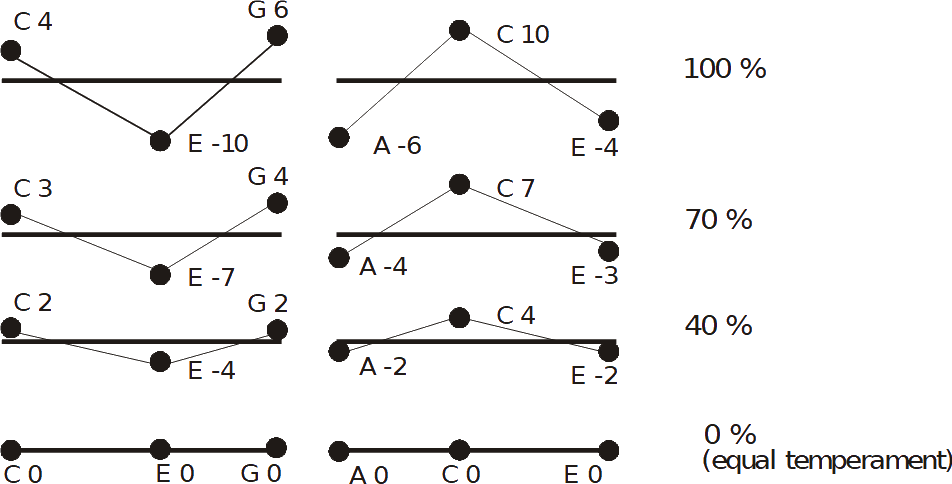
This program starts at every new note-on or note-off message. Subsequently it analyzes whether the harmonic situation allows to tune the tones to just intonation. If yes, it happens in real time, taking care that the retuning steps remain below the audibility and that the master tune level doesn’t drift too much away from its start position. A special feature of Hermode Tuning is the centered position of all retuned tones.

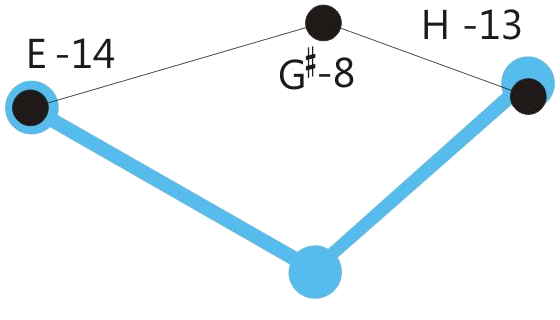
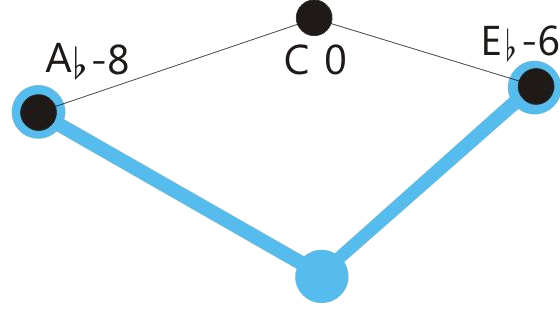
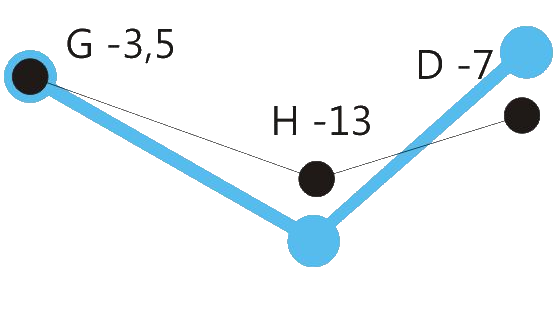
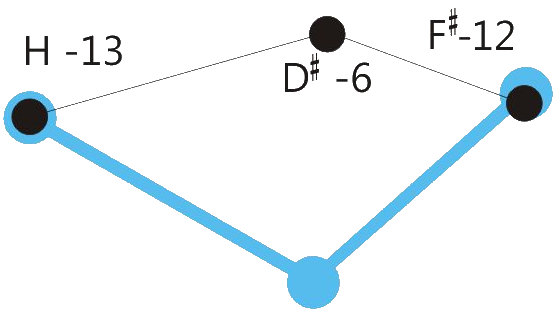
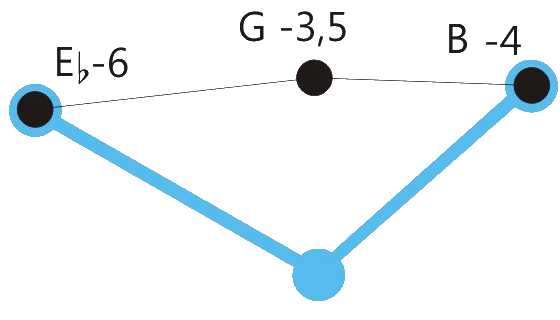
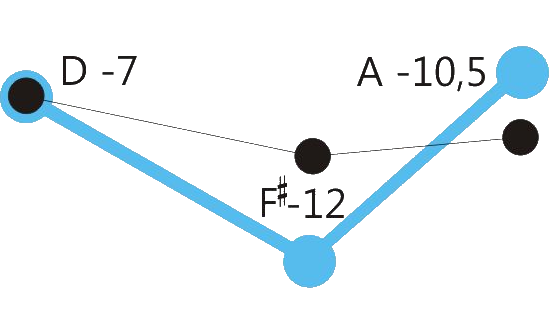
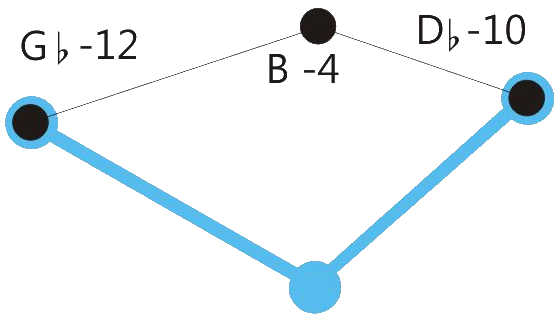
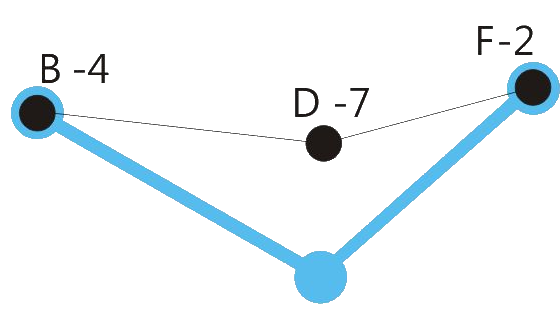
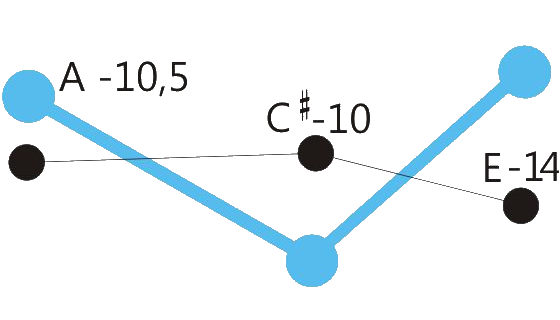
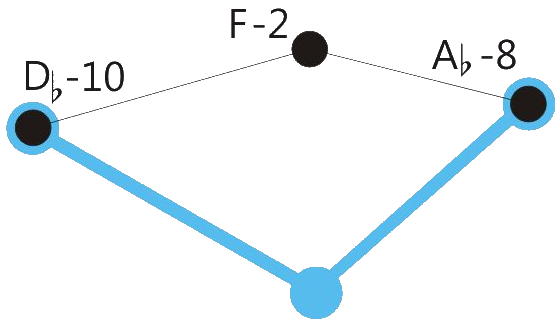
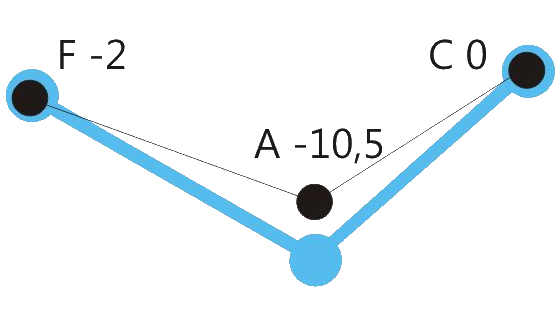
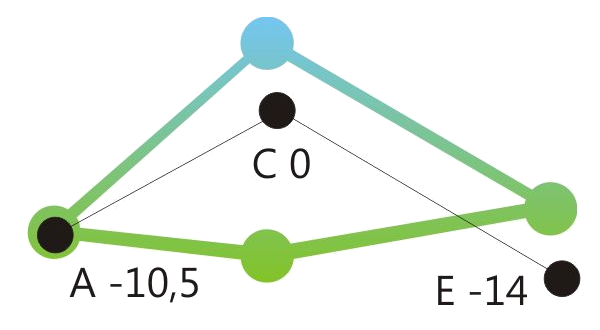
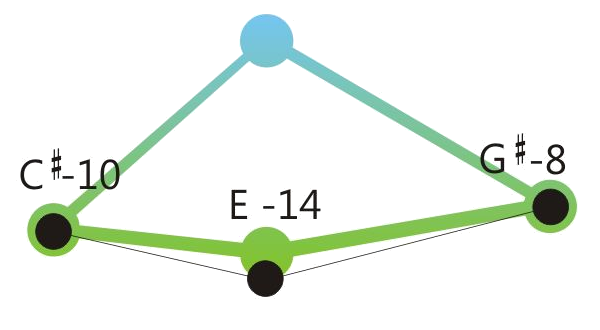
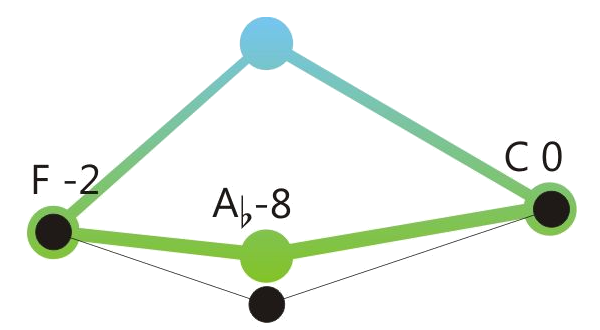
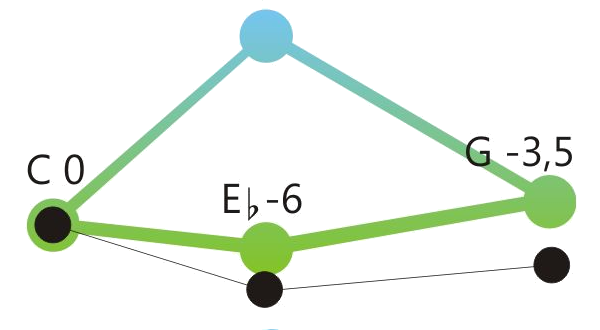
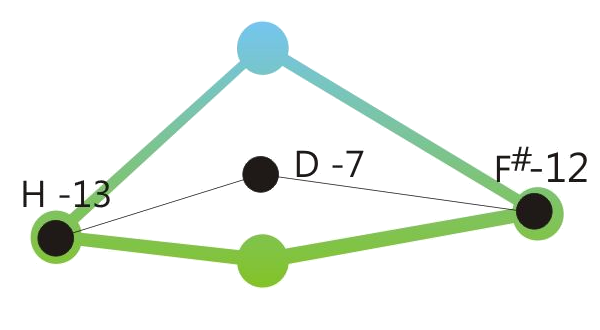
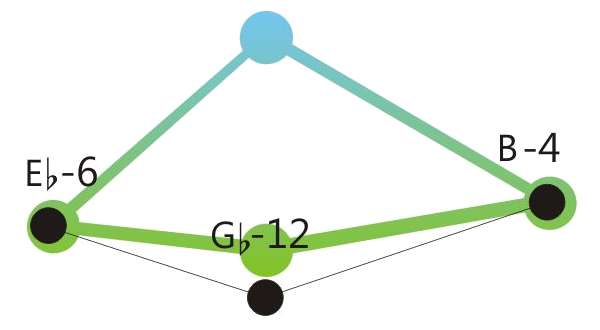
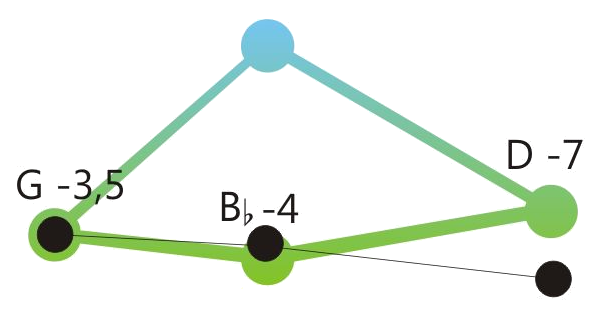
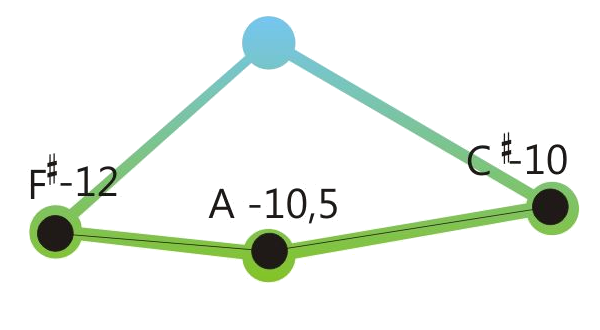
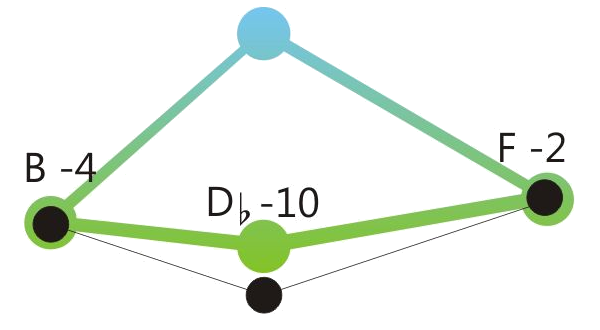
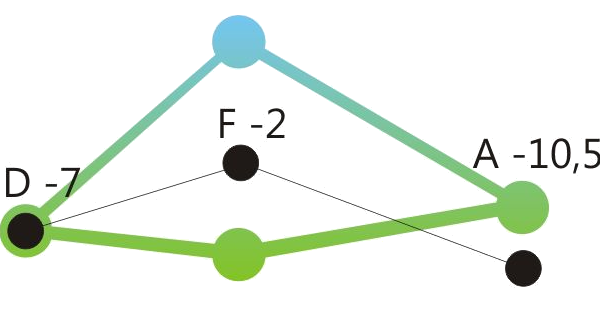
Centered position means: The sum of the retuning values of all retuned tones is close to zero. See the drawings below.

One of the program variations of Hermode Tuning tunes the seventh in dominant-seventh-chords to the so-called “natural seventh”. This sounds great, but due to the deep pitch of this seventh, some chord sequences like the here shown example shouldn’t be played legato.

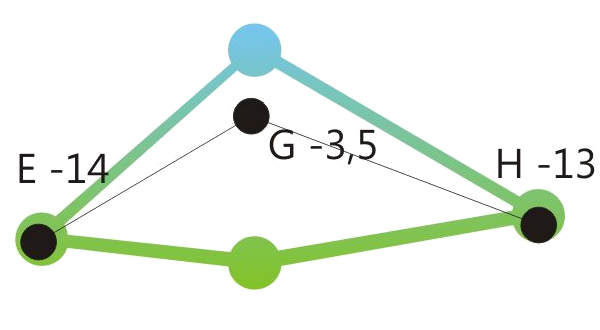
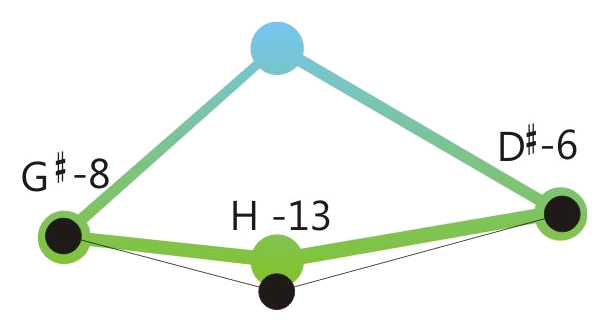
When making music together with equal tempered instruments or in situations where retuning steps will be audible, it could be advantageous to reduce the degree of tuning correction from 100 % to a lower value, e.g. 80 %. See the drawings below.

In the following we show to musical examples, each one illustrated by a diagram, showing the dynamic pitch control of Hermode Tuning. (Modus "Classic, 100 %"). The first one presents conventional harmonious sequences in C major. Nevertheless the tones "D" show very different positions:

The second example presents non-tonal harmonious sequences. For this reason and in order to avoid audible retuning steps, Hermode Tuning has to change continuously the mastertune level, shown by the thick black line.

At the Examples you will find musical examples with different tuning adjustments.